Graphs
Mar 052018A tree is an abstract idea, a common kind of structure which we find across many different applications. A tree models a relation between pairs of things:
- A section of an article contains another section,
- A directory contains another directory,
- An HTML tag contains other HTML tags,
- An employee manages another employee,
- A process spawns another process.
A “relation between pairs of things” is very abstract and very general — in almost any context, there are relations between pairs of things which we might want to model in a computer program. However, not every relation defines a tree structure.
Graphs vs. Trees
The following relations don’t define tree structures:
- A person is friends with another person.
- A Twitter user follows another user.
- A city is connected by a road to another city.
- A device is connected by a network cable to another device.
- A business buys from another business.
- A webpage links to another webpage.
- An academic paper cites another academic paper.
- A person has co-authored an academic paper with another person.
- A function calls another function.
- An object has a field referencing another object.
- A software package depends on another software package.
Each of these examples has “nodes” and “links”, but they are not trees; we call them graphs or networks.(1)
These example all define graph structures, but not tree structures:
- There is no “root node”, and it seems unnecessary to choose one.
- They may be “symmetric” — e.g. if two devices are connected by a network cable, neither is really the “parent” or the “child”.
- They may allow parts to be “unconnected” to each other — e.g. there is no sequence of roads connecting London to New York.(2)
- They may allow “cycles” — e.g. Alice is friends with Bob, Bob is friends with Charles, and Charles is friends with Alice.(3)
- They may allow “loops” — for example, this webpage links to itself.(4)
Notice that the same “nodes” can have different “links” depending on which relation we’re interested in. For example, if the “nodes” are people, then the friendship graph will be different to the co-authorship graph.(5)
Graph diagrams
Let’s see some examples; a node/link diagram is almost always the best way to visualise a graph structure, though there are other ways to represent graphs in text form and in computer programs.
This graph diagram shows the roads linking some towns and cities around Birmingham:
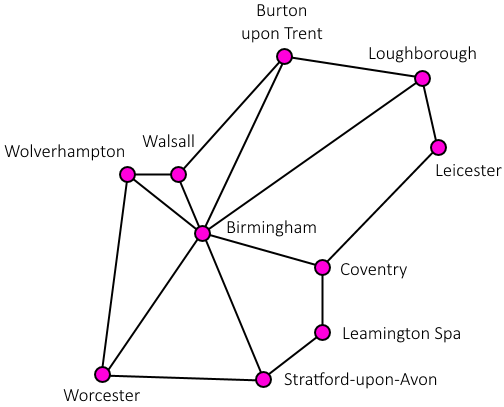
The purpose of this diagram is to show which towns and cities are connected by roads — the links represent the roads, but don’t accurately show their shape the same way a map would, since that information is not part of the graph.
This example shows some of the dependencies for the nano text editor:
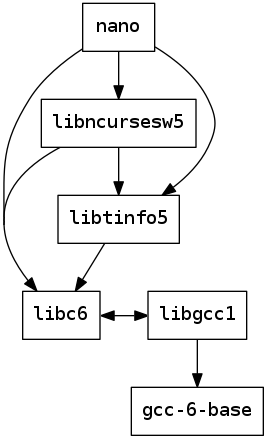
To install nano, all of these packages must be installed; but from the graph we can also determine which packages are necessary to install libtinfo5, for example.
The next example shows connections between audio sources and effects processors in a web audio application:
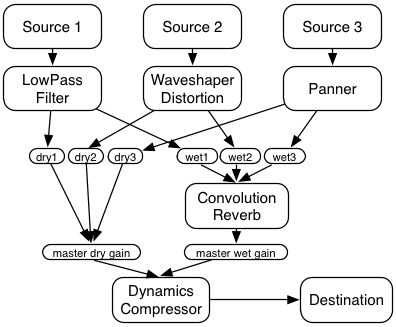
Image credit: W3C
The nodes represent audio sources, processors, and destinations; the links show which outputs should be routed to which inputs.
Graph definition
Examples are a good way to get intuition, but we should also define specifically what a graph is:
- A graph has nodes (or vertices) which are all the same type.
- A graph has links (or edges) between pairs of nodes.
There are some further rules we might add for graphs in some contexts:
- A graph might be directed if the edges have a “direction”. For example, a one-way street in a road network, or a Twitter user who follows someone without being followed back.
- The nodes and/or edges might have some data associated with them. For example, a link in a computer network has a transfer speed; a road in a road network has a length, a number of lanes, and speed limit.
- A graph might or might not allow cycles.(6)
It’s important to be aware of these differences, since they affect which data structures and algorithms we use to represent graphs and solve problems on them.
Graphs vs. Graph Diagrams
If two graphs have the same nodes and the same links between nodes, then they are the same graph. To draw a diagram for a graph, we have to choose positions for the nodes, but the positions are not part of the graph — they’re a feature of the graph diagram. Different diagrams can show the same graph:
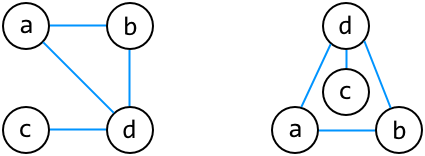
You can check this by writing down which pairs of nodes are connected by an edge in each diagram, then checking that both diagrams have the same edges.
Warning
The word “graph” is also used to mean the graph of a function, or charts such as bar charts or pie charts. None of these are graphs for our purposes.
Footnotes
- Some sources, especially in mathematics, consider a network to be a kind of graph where the nodes and/or links hold data. We aren’t interested in graphs without data, and “network” is often shorthand for “computer network”, so we will usually just say “graph”.
- In a tree, all nodes must be “connected” by a path to the root node, and therefore to each other.
- This can’t happen in a tree, because a root node has no parent, and is an ancestor of every other node. If there is a cycle A ↦ B ↦ C ↦ A then A’s parent is C, C’s parent is B, and B’s parent is A, so none of them can be a root node, yet they also have no other “ancestors”.
- In a tree, a node cannot be its own parent.
- It’s also interesting that the “nodes” of one graph can be “links” in another. For example, academic papers are nodes in the citation graph, but they are links in the co-authorship graph.
- A graph with no cycles is called acyclic.
Consider the examples:
- A cycle of friendship in a social network is fine.
- An academic paper can only cite another paper written earlier, so a cyclic citation graph is impossible (without time travel).
- A cyclic dependency graph means the package can’t be installed, because each package requires another to be installed first.
- A cycle in an audio processing graph would mean audio feedback, which might depend on which algorithm is used.


There are no published comments.