DS&A

Points and Vectors

Many computing applications deal with geometric or spatial data. Here are some of the more obvious examples:

• 3D graphics in games and movies,
• Geographic data in maps and sat-navs,
• Physical simulations in science, engineering, and games,
• Positions of buttons, labels and other components in GUI applications,
• Vector image formats,
• Page layouts of web pages and other media.

This means we need data structures for geometric data, and algorithms to solve geometric problems. As well as being applicable to a wide range of problems, they are good examples of how to design data structures to solve particular problems, and good practice for thinking about problems from the computer’s perspective.

In this post we’ll cover the fundamentals — points and vectors. To keep things simple, we’ll focus only on 2D examples.

Point

A point is simply a position in space. The usual way to represent a point in 2D space is with a pair of numbers, conventionally called x for the horizontal position and y for the vertical position.

Here’s a class for a 2D point in Python:

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y
    def __repr__(self):
        fmt = 'Point({!r}, {!r})'
        return fmt.format(self.x, self.y)

There is a bit more to it than this, though: we need to specify what x and y actually mean. To some extent, this is obvious — but there are still some choices to make. Consider the model below:

To specify what x and y represent, we need to decide what origin to measure from, what units to measure in, and which directions are positive and negative. Usually, these choices are made to simplify whatever problem we’re working on; the model above shows some of the common options.(1)

Vector

A vector is a lot like a point — a 2D vector has x and y components. However, there are two conceptual differences:

• A vector represents a displacement between two points, or can represent a single point as a displacement from the origin.
• Vectors support arithmetic operations including vector addition and scalar multiplication.(2)

Displacements

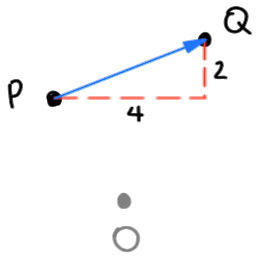
Consider the two points called P and Q below:

class Vector:
    def __init__(self, x, y):
        self.x = x
        self.y = y
    def __repr__(self):
        fmt = 'Vector({!r}, {!r})'
        return fmt.format(self.x, self.y)

So far, the Vector and Point classes are identical, except for their names. The difference is in interpretation: a point is a position in space, whereas a vector is the relative displacement from one point to another. But it’s no coincidence that they have the same data: the coordinates of a point are equal to the components of a vector from the origin to that point.

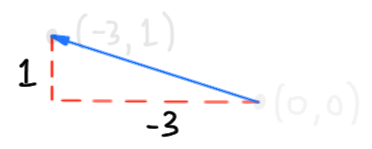
Addition

Another difference between points and vectors is what we can do with them. It doesn’t really make sense to “add” two points together, but we can add vectors:

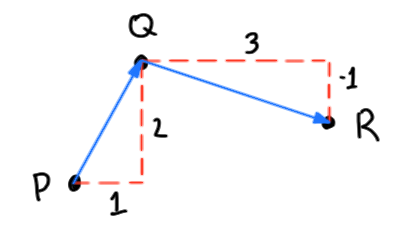
The general rule is that P-to-Q + Q-to-R = P-to-R. But to calculate the result, we don’t need to draw pictures; using the x and y components of the vectors, we can write:

This makes sense because if we go from P to R via Q, we go a total of 1 + 3 = 4 units horizontally; vertically, we go 2 units up and 1 unit down, for a total of 1 up.(4) So we can implement vector addition by adding the components together:

class Vector:
    # ...
    def add(self, other):
        return Vector(self.x + other.x, self.y + other.y)

Just like the equation above, the inputs are two vectors, self and other, and the output is another Vector. Try it out:

>>> a = Vector(1, 2)
>>> b = Vector(3, -1)
>>> a.add(b)
Vector(4, 1)

Subtraction

It also makes sense to “subtract” one vector from another:

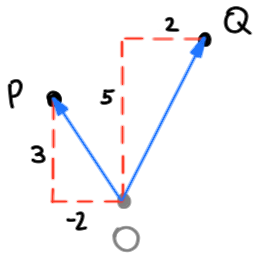
In this diagram, we’re thinking of P and Q as points, and also as vectors from the origin. The general rule is that Q − P = P-to-Q. As with addition, we can calculate the result using the vector components:

Here’s an implementation in Python:

class Vector:
    # ...
    def subtract(self, other):
        return Vector(self.x - other.x, self.y - other.y)

The inputs are the two vectors self and other, and the output is a new vector. Try it out:

>>> p = Vector(-2, 3)
>>> q = Vector(2, 5)
>>> q.subtract(p)
Vector(4, 2)

Scalar multiplication

Another thing we can do with vectors is scale them — make them longer or shorter by some factor:

Again, the picture shows the geometric meaning of this operation, but we can compute the result numerically:

That is, to scale a vector by a factor of 3, simply multiply each component by 3. The inputs to this operation are a vector and a scale factor (usually called a scalar), and the output is a new vector. Here’s an implementation in Python:

class Vector:
    # ...
    def scale(self, scalar):
        return Vector(scalar * self.x, scalar * self.y)

Try it out:

>>> a = Vector(2, 1)
>>> a.scale(3)
Vector(6, 3)

Length

If a vector is the displacement from one point to another, then the length of the vector is the distance between those two points:

We can calculate the length using Pythagoras’ theorem:

In Python:

from math import sqrt

class Vector:
    # ...
    def length(self):
        return sqrt(self.x ** 2 + self.y ** 2)

Try it out:

>>> a = Vector(4, 3)
>>> a.length()
5.0

Vector class

Putting it all together, our entire Vector class is given below:

from math import sqrt

class Vector:
    def __init__(self, x, y):
        self.x = x
        self.y = y
    
    def __repr__(self):
        fmt = 'Vector({!r}, {!r})'
        return fmt.format(self.x, self.y)
    
    def add(self, other):
        return Vector(self.x + other.x, self.y + other.y)
    
    def subtract(self, other):
        return Vector(self.x - other.x, self.y - other.y)
    
    def scale(self, scalar):
        return Vector(scalar * self.x, scalar * self.y)
    
    def length(self):
        return sqrt(self.x ** 2 + self.y ** 2)

By combining operations, we can do things like find the distance from P to Q:

>>> p = Vector(5, 3)
>>> q = Vector(8, 5)
>>> q.subtract(p).length()
3.605551275463989

Footnotes

1. Typically, these choices have already been made by whichever library or API we’re using.
2. Recall that a type defines not just what data is represented, but also what operations are supported.
3. Assuming that upwards is the positive vertical direction.
4. We do have to check this — just because we called it “addition” doesn’t automatically mean that adding the vectors’ components is the right way to calculate it.

• Tags: 
• geometry, data structures

Comments

Chris Gray25 April, 2018Gonna need some help on this one. Interesting blog. :-)